 |
Figura 4.23. Distribución de saturación con
distancia según Calhoun".
|
Igualando las ecuaciones 4.41 y 4.42 y sustituyendo las ecuaciones 4.43 y 4.44, se tiene:
AI resolverse esta expresión, se obtiene:
 |
Figura 4.23. Distribución de saturación con
distancia según Calhoun".
|
 |
Figura 4.22. Distribución de saturación con
distancia según Buckley y Leverett.
|
 |
Figura 4.20. Derivada del flujo fraccional en
función de saturación de agua (según Ferrer). |
 |
Figura 4.19. Pendiente a la curva de flujo fraccional a diferentes
saturaciones
de agua. |
 La consideración anterior, así como los resultados de laboratorio, han permitido
llegar a la conclusión de que el frente de invasión no es plano, tal como se ha venido
considerando hasta ahora, sino que es una zona de extensión y forma definida que se
mantiene con el tiempo. Esta zona o región se estabiliza al poco tiempo de comenzar
la inyección, por lo que se acostumbra denominarla zona estabilizada.
La consideración anterior, así como los resultados de laboratorio, han permitido
llegar a la conclusión de que el frente de invasión no es plano, tal como se ha venido
considerando hasta ahora, sino que es una zona de extensión y forma definida que se
mantiene con el tiempo. Esta zona o región se estabiliza al poco tiempo de comenzar
la inyección, por lo que se acostumbra denominarla zona estabilizada.
 |
Figura 4.14. Tasa másica de flujo a través de
un elemento lineal de volumen AO Ax.
|
 |
Figura 4.12. Efecto de la viscosidad del petróleo sobre el flujo
fraccional de
agua (según Smith y Cobb). |
 |
Figura 4.13. Efecto de la viscosidad del
agua sobre el flujo fraccional de agua. |
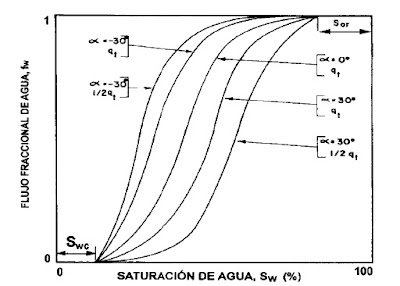 |
Figura 4.11. Efecto de la tasa de inyección
sobre el (lujo fraccional de agua (según Smith).
|
 Luego, como se muestra en la Figura 4.9, el efecto de la presión capilar es aumentar fw.
Es por esto, que en una invasión con agua, es deseable disminuir o eliminar el gradiente de presión capilar, lo cual puede realizarse alterando la humectabilidad de la
roca o eliminando la tensión interfacial entre el petróleo y el agua.
Luego, como se muestra en la Figura 4.9, el efecto de la presión capilar es aumentar fw.
Es por esto, que en una invasión con agua, es deseable disminuir o eliminar el gradiente de presión capilar, lo cual puede realizarse alterando la humectabilidad de la
roca o eliminando la tensión interfacial entre el petróleo y el agua.
 |
Figura 4.8. Flujo fraccional de agua en función
del ángulo de buzamiento de la formación. |

 la
tasa de inyección (q1) el gradiente
de presión. Si la tasa total de flujo es constante, y si se supone que el desplazamiento de petróleo se lleva a cabo a temperatura constante, entonces las viscosidades del agua y del petróleo tienen un
valor fijo y la ecuación simplificada del
flujo fraccional es estrictamente función de saturación de agua. Para una
serie de valores típicos de permeabilidades relativas, como se presentan en
la Figura 4.6, la curva de fu, vs Sw cuando se hace cero el gradiente de presión capilar
en la ecuación 4.10 tiene forma de S invertida como se muestra en la Figura 4.7, con
saturaciones límites entre S^ y (1-Sw) entre los cuales el flujo fraccional aumenta
desde cero hasta uno. La curva de flujo fraccional es de gran utilidad en la predicción y
análisis del comportamiento de yacimientos durante una invasión de agua o de gas.
la
tasa de inyección (q1) el gradiente
de presión. Si la tasa total de flujo es constante, y si se supone que el desplazamiento de petróleo se lleva a cabo a temperatura constante, entonces las viscosidades del agua y del petróleo tienen un
valor fijo y la ecuación simplificada del
flujo fraccional es estrictamente función de saturación de agua. Para una
serie de valores típicos de permeabilidades relativas, como se presentan en
la Figura 4.6, la curva de fu, vs Sw cuando se hace cero el gradiente de presión capilar
en la ecuación 4.10 tiene forma de S invertida como se muestra en la Figura 4.7, con
saturaciones límites entre S^ y (1-Sw) entre los cuales el flujo fraccional aumenta
desde cero hasta uno. La curva de flujo fraccional es de gran utilidad en la predicción y
análisis del comportamiento de yacimientos durante una invasión de agua o de gas.