Criterio de Mohr - II

La falla no tendrá lugar cuando los valores de a y T estén por debajo de la curva AB. La falla tomará lugar si el círculo con centro C con un diámetro a} y ar3toca a la curva AB. La envolvente de Mohr es usualmente cóncava hacia abajo, de tal manera que a medida que el esfuerzo promedio se incrementa el plano de fractura se torna más inclinado en dirección creciente a a,.El punto en el cual la envolvente de Mohr intersecta al eje r es la resistencia al cizallamiento de la roca. La figura 24 es una envolvente típica de Mohr mostrando varias pruebas.

La expresión matemática relaciona a la resistencia al cizallamiento con las fuerzas de contacto, la fricción y la cohesión que existe entre los granos. Una aproximación lineal de la curva AB es:

Donde Im es el índice friccional y Is es el índice de intacto. Ambos son dependientes del material.| Este criterio correlaciona razonablemente a la falla quebradiza pero da pobres resultados con fallas dúctiles. Los parámetros Im, Is y Co se determinan en el laboratorio. De manera general, para rocas débiles Im es menor a 0.1, Is es menor a 0.0001; sin embargo, para rocas duras Im varía de 5 a 15 y Is es igual a 1.

Criterio de Mohr - I

En 1900 Mohr propuso que cuando una falla por cizallarmento sucede en un plano, el esfuerzo normal y de cizallamiento en ese plano se da en función de las características del material. El diagrama de Mohr es probablemente el método gráfico más importante para representar la variación de los esfuerzos en dos dimensiones, la figura 22 ¡lustra el círculo de Mohr.

El primer paso es dibujaren coordenadas cartesianas donde el eje y representa al cizallamiento y el eje x

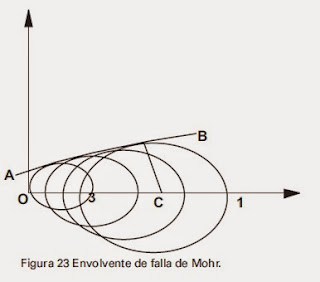
La manera en que se usa el círculo de Mohr es a través del trazo de varios círculos con base en los datos obtenidos de una serie de pruebas triaxiales. Las pruebas triaxiales se llevan a cabo bajo diferentes presiones de confinamiento hasta que la falla ocurre y se obtiene una envolvente de falla particular para cada tipo de roca. De aquí se define que los esfuerzos normales y de cizallamiento están normalmente relacionados de tal forma que r=f(a). La figura 23 muestra cómo esta relación está representada como al curva AB.

Criterios de falla

Existe una relación entre el esfuerzo principal efectivo, el cual representa el límite a partir del cual la inestabilidad o la falla ocurre. Si la roca se encuentra bajo confinamiento estos esfuerzos serán máximos. La variación del esfuerzo máximo (a1) con la presión de confinamiento (o3) se conoce como criterio de falla. Existen varios criterios de falla en la literatura, aquí sólo se presentará el panorama general de cada uno de ellos. Para mayor profundidad en el tópico refiérase a la bibliografía reportada.

Esfuerzos efectivos

Al aplicar un esfuerzo total en una porción de roca que contenga fluidos, parte de éste será soportado por el fluido contenido en los poros. Como el fluido soporta parte del esfuerzo, la matriz de la roca sólo está afectada por la componente del esfuerzo efectivo. Al ocurrir el movimiento de fluidos en un yacimiento ocurre un efecto en la respuesta mecánica. La difusión del fluido en los poros también alterará los resultados, por lo tanto, puede haber una gran diferencia en los resultados si las pruebas se realizan en condiciones drenada y no drenada. La velocidad a la cual se aplique la carga a una muestra porosa puede hacer que la roca se comporte de una manera rígida o suave. El concepto de esfuerzo efectivo fue introducido originalmente por Terzaghi en 1923, cuando sugirió una relación lineal entre el vacío del material y el logaritmo de la presión aplicada.

Y gobierna la deformación del medio poroso mientras la falla se controla por el esfuerzo efectivo dado en la ecuación 5.3.4.4.1. Típicamente el valor de a es 0.7.

Efecto de! módulo de Poisson - III

Por definición, la fuerza es positiva. De tal forma que en el caso de el cambio lateral, o deformación principal (e2), debe ser negativo porque el cambio es en expansión. El esfuerzo aplicado para causar compresión es en este caso a\ y es positivo; por lo tan to, la otra deformación principal llamada 1 es contracción y tiene signo positivo. La relación de la expansión lateral a la contracción longitudinal es la relación de Poisson y se expresa como:

Efecto de! módulo de Poisson - II

La curva esfuerzo/deformac¡ón(a) es lineal para la mayoría de las rocas y finaliza en forma abrupta en el punto F. Anteriormente se mencionó que la relación lineal esta representada por E (módulo de Young). Sin embargo, esta relación sólo es cierta si el material es linealmente elástico. La figura 20 muestra que la curva tiene varias regiones antes de la falla. La figura (b) muestra un material perfectamente elástico. Esto está definido por una única relación entre el esfuerzo y la deformación que no necesita ser lineal. 

La elasticidad perfecta se tiene cuando el material se somete gradualmente a un esfuerzo y cuando se libera éste la ruta sigue la misma tendencia en sentido inverso. Además, la energía almacenada en la carga se disipa en la descarga. Por lo tan- to, no hay un modulo único, sino que para cualquier valor correspondiente a un punto P, la pendiente PQ de la tangente a la curva es el modulo tangente de Young y la pendiente de la secante OP, ole, se llama el módulo secante. 

La figura c muestra el comportamiento del material elástico. Un material se llama elástico si después del esfuerzo y liberación, antes de la falla, la deformación va a cero, aunque no necesariamente por la ruta de carga. Este efecto se llama histeresis y es causado por la disipación de energía de procesos tales como la creación de nuevas microfracturas. Al inicio se mencionó que una fuerza compresiva aplicada en un cilindro de roca causará deformación. Si la roca se comprime en una dirección, se acortará en esa dirección y se expandirá en forma lateral. La figura 21 ¡lustra el cambio en diámetro con el cambio de longitud debido a una fuerza compresional.

Efecto de! módulo de Poisson - I

Un espécimen de roca, tal como un cilindro cuya longitud es de dos a tres veces su diámetro, se deformará cuando esté sujeto a compresión axial. Entre más alto sea el nivel de esfuerzos, mayor deformación experimentará la roca. Las deformaciones axiales y laterales para cualquier campo de esfuerzos aplicado, se pueden medir con manómetros de deformación fijados a la muestra de roca. La gráfica del esfuerzo aplicado contra la deformación producirá una curva similar a la de la figura 19.

Esta curva tiene distintas regiones. En la región no lineal (OA) la roca tiende a comprimirse debido a las microfracturas preexistentes que se cierran y a los minerales que se comprimen ligeramente. Si la roca se removiera, la mayoría de las microfracturas permanecerían cerradas y resultaría en una deformación neta. La porosidad de las fracturas está relacionada con esta deformación. Continuando con la aplicación de carga (A a B), la mayoría de las fracturas cerradas producen la compresión neta de la roca y donde los poros se deforman y los granos se comprimen a un ritmo lineal. Esta forma lineal se representa por un coeficiente de proporcionalidad, E, el cual se llama módulo de Young y se define como:

La mayoría de las rocas presentan esta respuesta en un amplio rango de carga y, por lo tanto, el módulo de Young es una medición de la rigidez de la roca o el parámetro que expresa la resistencia a la deformación que una tiene para una determinada condición de carga. Continuando más allá del punto B con la aplicación de la carga, se origina un daño que no es reversible debido a que ocurren grandes deformaciones y el módulo total es más alto. De esta manera la descripción del comportamiento de la roca se vuelve más difícil usando un modelo elástico constante. Sin embargo, el uso de una secante así como un módulo tangente pueden hacerlo más sencillo. La diferencia en esos dos módulos puede ser significativa y debe tenerse cuidado al utilizar los datos reportados. Una forma más clara de visualizar la relación esfuerzo/deformación se tiene al analizar la figura 20 (a, b y c).