Ecuación de avance frontal o ecuación de la velocidad del frente de invasión - III

Igualando las ecuaciones 4.18 y 4.20 se obtiene el cambio del volumen de agua a un determinado tiempo en función del cambio experimentado por la fase agua a ese mismo tiempo:

Sustituyendo la ecuación 4.23 en la ecuación 4.21, resulta la expresión siguiente:

Esta ecuación da la saturación de agua como una función de tiempo en el punto x, dentro del sistema lineal, pero la expresión que se requiere es la de saturación de agua como una función de x a un determinado tiempo t. Como se conoce que Sw es, en forma general, una función de x y t, se puede escribir:

Por tanto, si de la ecuación 4.25 se toma la derivada total de la saturación de agua, resulta:

Ecuación de avance frontal o ecuación de la velocidad del frente de invasión - II

La cantidad de agua que existe en un elemento Ax de la formación a un tiempo t, viene dado por:

y la tasa de acumulación de agua será el cambio de este volumen de agua con respecto al tiempo, es decir:

La variación del volumen de agua con respecto al tiempo, también puede calcularse si se hace un balance de materiales para el elemento Ax de la formación. Así se tiene: 

La variación del volumen de agua con respecto al tiempo, también puede calcularse si se hace un balance de materiales para el elemento Ax de la formación. Así se tiene:

por lo tanto

Ecuación de avance frontal o ecuación de la velocidad del frente de invasión - IV

Como se desea obtener la distribución de saturación en el yacimiento a un determinado tiempo, es necesario considerar el movimiento de una saturación Sw en particular. Entonces, si se fija un valor de Sw, esto implica que dSw - 0 y, por consiguiente:

Si se despeja el cambio de saturación con tiempo, se tiene:

Combinando las ecuaciones 4.24 y 4.28, se obtiene:

Como el flujo total es constante, el flujo fraccional no depende de tiempo, esto implica que:

La ecuación 4.32 es la ecuación de la velocidad de un frente de saturación constante, la cual implica que, para una tasa constante de inyección de agua (g,), la velocidad de avance de un plano de saturación de agua constante es directamente proporcional a la derivada de la ecuación de flujo fraccional evaluada a esa saturación. Si se considera insignificante el gradiente de presión capilar en la ecuación 4.8, entonces el flujo fraccional es estrictamente una función de la saturación de agua, indistintamente de si se incluye o no el término de gravedad: de allí, el uso de la diferencial total del flujo fraccional fw, en la ecuación de velocidad. 

Tal como fue deducida, la fórmula de la velocidad de avance del frente de invasión sólo se aplica a la zona situada detrás del frente que precisamente constituye la región de interés, puesto que delante del frente se supone que las saturaciones permanecen constantes.

Ecuación de avance frontal o ecuación de la velocidad del frente de invasión - I

En 1942 Buckley y Leverett presentaron la ecuación básica para describir el desplazamiento inmiscible en una sola dimensión2. Si se considera que el agua está desplazando al petróleo, la ecuación determina la velocidad de avance de un plano de saturación de agua constante que se mueve a través de un sistema poroso lineal, en el cual se está inyectando un fluido a una tasa q,. Aplicando la ley de Conservación de la Masa al flujo de fluidos (agua y petróleo) en la dirección x, a través del elemento de volumen AijiAx de la formación, representado esquemáticamente en la Figura 4.14, se tiene:

Figura 4.14. Tasa másica de flujo a través de un elemento lineal de volumen AO Ax.

Viscosidad del agua

Si la viscosidad del agua aumenta, el flujo fraccional del agua disminuye y la eficiencia de desplazamiento será mayor. Este efecto puede alcanzarse, por ejemplo, con la adición de ciertos polímeros al agua, pero hay que tener en cuenta que un aumento de viscosidad puede disminuir la inyectividad. La Figura 4.13 representa el efecto de la viscosidad del agua.

Figura 4.12. Efecto de la viscosidad del petróleo sobre el flujo fraccional de
agua (según Smith y Cobb).

Figura 4.13. Efecto de la viscosidad del
agua sobre el flujo fraccional de agua.

Viscosidad del petróleo

Si se inyecta el agua buzamiento arriba y se consideran insignificantes los efectos de presión capilar, el flujo fraccional aumentará a medida que la viscosidad del petróleo aumenta, lo cual conduce a altos valores de fw y, por consiguiente, a que el desplazamiento de petróleo sea menor. La Figura 4.12 representa el efecto de la viscosidad del petróleo.

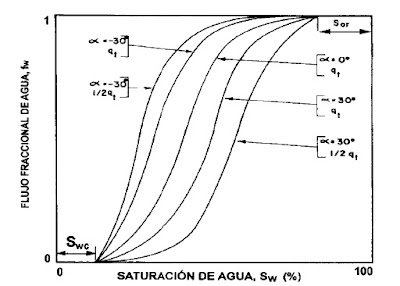Figura 4.11. Efecto de la tasa de inyección sobre el (lujo fraccional de agua (según Smith).

Tasa de Inyección

El efecto de la tasa de inyección depende de si el agua se mueve buzamiento arriba o buzamiento abajo. Como el objetivo es minimizar fw, se observa en la ecuación de flujo fracciona! que la tasa de inyección q, debe tener un valor bajo. 

Si el agua se mueve buzamiento abajo, será mejor inyectar a altas tasas. Desde un punto de vista práctico, la tasa de inyección es controlada por la economía del proyecto y por las limitaciones físicas del equipo de inyección y del yacimiento. La Figura 4.11 representa el efecto de la tasa de inyección.